Using Hyperopt to Tune Trading Bot Hyperparameters
Writing simple trading bots, or algorithms, to trade a cryptocurrency, commodity, or stock is pretty simple, right? You just need to buy low and sell high... easy, right?
Well as anyone who has attempted to do this will tell you, it's not that simple, as there are a myriad of complexities. In this post I'll talk about just one aspect, and that is 'hyperparameter tuning'. I'm going to slightly abuse the term hyperparameter here for this example. Typically, a hyperparameter is term used in machine learning to describe a 'meta parameter'. That is, not the parameters that the machine learning algorithm itself is learning, but the parameters about the learning as a whole.
An analogy: what books I decide to read at university in order to learn might be a parameter, but what university I go to in order to do that might be a hyperparameter.
In this post I'm talking about using a python library called hyperopt to tune the parameters of a simple trading algorithm. So we are actually tuning parameters, not hyperparameters, but the library doesn't care. Hopefully this will become clear below. Just think of it as trying to tune some parameters.
Lets say we devise a very simple trading strategy to instruct some software to automatically trade a currency (or cryptocurrency, stock, commodity, etc):
Buy when the price goes above the 21-period moving average, sell when it goes below it.
Pretty simple, huh? The aim is to try and detect some kind of trend in the movement.
In that algorithm, "21" is a (hyper)parameter. It could be 18, or 53, or 1, or 10,000. How do we choose the best one to ensure that our algorithm is profitable? Too small and the algorithm will trade too much and likely lose money in fees. Too big and we'll only trade once in a blue moon and by then the price will have already moved quite a lot.
What does the problem look like?
Let's take some guesses and plot them out and see what they look like. In the charts below I'm plotting the price of USD/JPY and a 5 period moving average. The green triangles indicate where the price rises above the moving average and we should buy. The red ones when we go below and should sell.
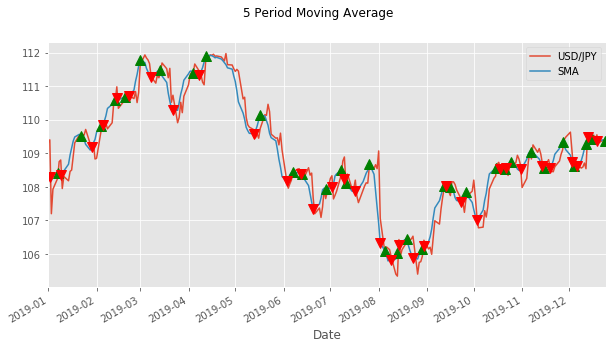
Quite noisy. Lots of trades going on. And we will be charged a commission on each trade, so will lose a small amount each trade. Let's look at a few more:
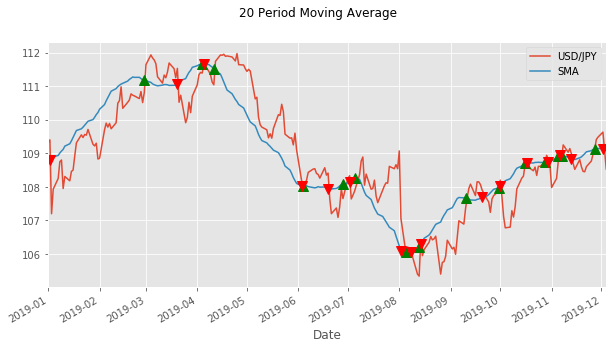
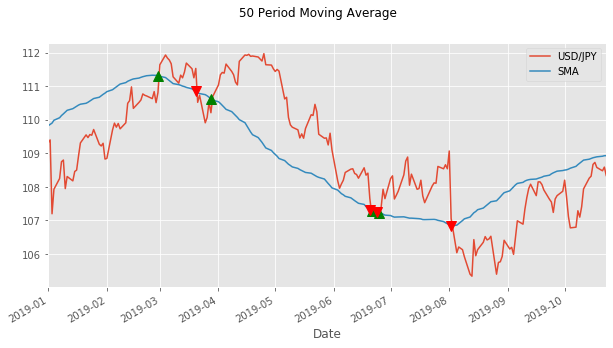
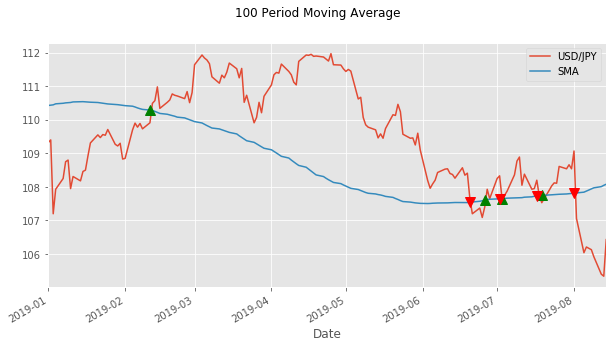
As you might be able to see we do really badly on some of them. Look at the last one. We buy in mid-February at around 110.2 Yen and then sell in mid-June at a lower price of around 107.5 Yen... not what we want to do!
What can we do?
So what is the best number to use? What is the best figure for a moving average that we should use? That is where the parameter tuning comes in.
We could just try every number. Computers are fast, right? Try every number between say 4 and 200 and see what works best. That is only 196 possible outcomes. This is known as a 'brute force' approach. That will take a computer less than a second to work out.
But what if our strategy is more complex? What if we have several parameters we need to tune simultaneously? Rate of upward trend, rate of downward trend, stop loss position, etc? We could quickly end up with hundreds of thousands or even millions of combinations to try out. And what if we are wanting to test on several years of data? Maybe using 5-minute intervals, not daily intervals? What if each attempt takes longer as we are testing out our SuperFancyUltimateMoneyMaker2000 strategy?
Brute force won't cut it. We could be waiting for hours, days or weeks for a computer to try all possible combinations.
So what if it could do something more clever? What if it could try some random combinations and then look to see if they give good results or not, and if they do, then try other values 'near' those other good ones.
This is what Hyperopt lets us do. It uses an algorithm called Tree-structured Parzen Estimator (TPE) to more intelligently 'search' the space of all possible combinations to find the best ones. The end result is something that could take a whole day to search all best combinations by the brute for approach can now take mere minutes.
And what is great with Hyperopt is that it is really simple to use it. You need to define two things:
- Your function that you want it to run. In this case a function that simulates trading as detailed above and takes one or more parameters you want to optimise.
- The parameter space.
Below I'll dive into the actual code and the results of the optimisation we did. If you are not a Coil subscriber, now will be a good time to subscribe ;)
Header photo by Mikael Kristenson on Unsplash
